One day in 2005 while riding two abreast in the bike lane, a small rock flew out from beneath my rear tire and hit my partner*s chain stay. I apologised and she explained that it was just a tire bullet. I had seen them before, but never knew they had a name. Later I realized that I didn*t really know anything about them from a physical standpoint, so I looked online for some basic information. I didn*t find anything on the cycling forums or anywhere on the web. I even looked for information about the forces involved in tiddly winks, which have the same basic mechanism. Having found nothing at all, here is my own analysis:

Mechanism:
Since the rocks shoot out at high velocity, I assume the tire does not simply hit the rock and push it aside, but stores up energy in tire deformation which is suddenly released. The tire must run over the top of the rock for the tire to deform. At the point of maximum tire deformation, I suspect that the force on a spherical rock is proportional to both the tire pressure and the cross-sectional area (square of the diameter) of the rock. Also, the rock must have access to the outside. If the tire covers the rock completely, it cannot fly out.

Launch Direction:
If the rock is launched at or near the point of maximum force, that would be when it is under the contact patch of the tire. The front/rear forces would then be the same and cancel out, leaving a net force out to the side. This matches most of my observations, straight out to the side. If the rock launched before maximum force was reached, it would shoot out a little toward the forward direction, and if it launched as the contact patch was lifting, the rock would shoot out a little toward the rear. And indeed, I have seen some fly out at an angle, but not more than about 20 degrees either way.

Launch Angle:
The force on the rock certainly has a downward component, but cannot travel that direction because of the road. It can only travel out to the side and upward. If it starts out traveling parallel to the road while still touching the road, it will hit something and bounce upward at some angle. Is there a characteristic launch angle for rock bullets? Do the ones with low trajectories go unnoticed? My friend and I were about 3 feet apart, and her chain stay was about 1 foot high, so the angle = ATAN(1/3) = 18.4 degrees.

Size Limitations:
Obviously, cyclists do not run over big rocks for fear of pinch flats, but what about the smaller rocks? Do they get launched, too, or do they just go unnoticed? Is there a characteristic size for a rock bullet? The most common size (of those I notice) is around .25 to .45 inch.

My First Experiment:
While watching the 2005 Tour de France, during the commercials I experimented by sticking small objects between my rear tire and the metal roller on my trainer while slowly turning the tire. (What some people will do for fun!) The best object I found was a white plastic airsoft BB (6 mm diameter) with a couple of flats filed on opposite sides. If I got it just right, it would shoot out the side at high velocity, even though I was barely turning the wheel. That observation made me absolutely certain that the tire pressure governs the velocity. I wanted to measure the angle and distance, but the BB always hit the side of the flywheel. Since it did hit, however, that constrains the angle to be less than about 45 degrees.

My Second Experiment:
In 2014 I used an Instron at my workplace to push a "rock" (a rod 0.45 inches in diameter) into the sidewall of a bicycle tire inflated to 100 psi. The machine measured the load (force) vs extension (deflection) of the rod as it slowly deformed the tire. In the plot below, the trace starts at the upper right. There is a short horizontal line that corresponds to zero load before the rod met the tire. At 0.15 inches, the rod touched the tire, and the load started to increase. Actually, instead of rising, the load went downward because the machine considered that to be the negative direction. So the trace continued down and to the left until the load cell maxed out at 100 lbf.

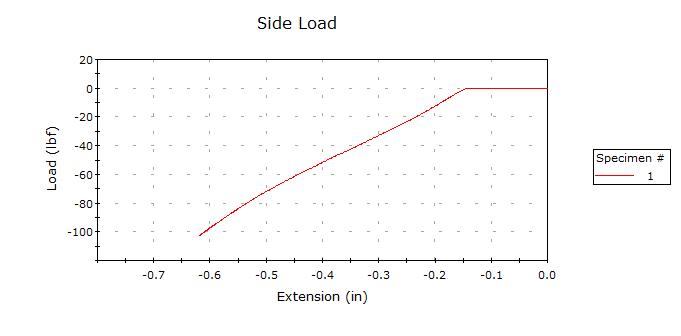
I was very pleased to see a nice straight line! That meant the force was proportional to the deflection and therefore followed Hook*s Law. The system acts just like a coil spring. The slope of the line is called the spring rate or spring constant k. So k is 85 pounds in 0.4 inches, or 212.5 lb/in. That is a stiff spring! It would take 212 pounds to compress that spring just one inch. The potential energy stored by a spring is k*x*x/2 where x is the amount of compression or deflection. The kinetic energy of a moving object is m*v*v/2 where m is the mass and v is the velocity. Since both equations are for energy, they can be set equal to each other and solved to find the velocity. I solved for the case of a 0.45 diameter "rock" with specific gravity of 2.5 (limestone, 1.9 grams), that deforms the tire until it is completely covered, and assumed that all the energy stored in tire deformation was released as kinetic energy. The result? The rock would fly out at 50 meters per second, or 112 mph!

Well, I hope you have fun thinking about rock bullets! I sure did! Please share your tire bullet observations!